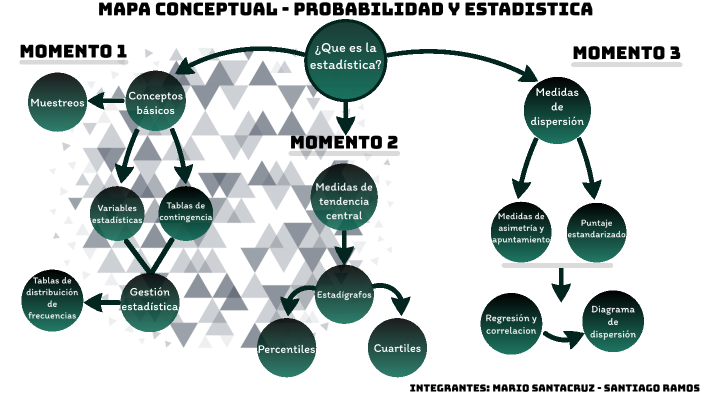
Mapa Conceptual De Probabilidad Y Estadística

Vamos a construir un mapa conceptual de Probabilidad y Estadística. Lo haremos por partes. Primero, definiremos los conceptos centrales. Luego, las conexiones entre ellos.
Parte 1: Conceptos Fundamentales
Probabilidad es la medida de la posibilidad de un evento. Se expresa como un número entre 0 y 1. Cero indica imposibilidad, uno indica certeza.
Un evento es un subconjunto de un espacio muestral. El espacio muestral es el conjunto de todos los resultados posibles. Cada resultado es un evento simple.
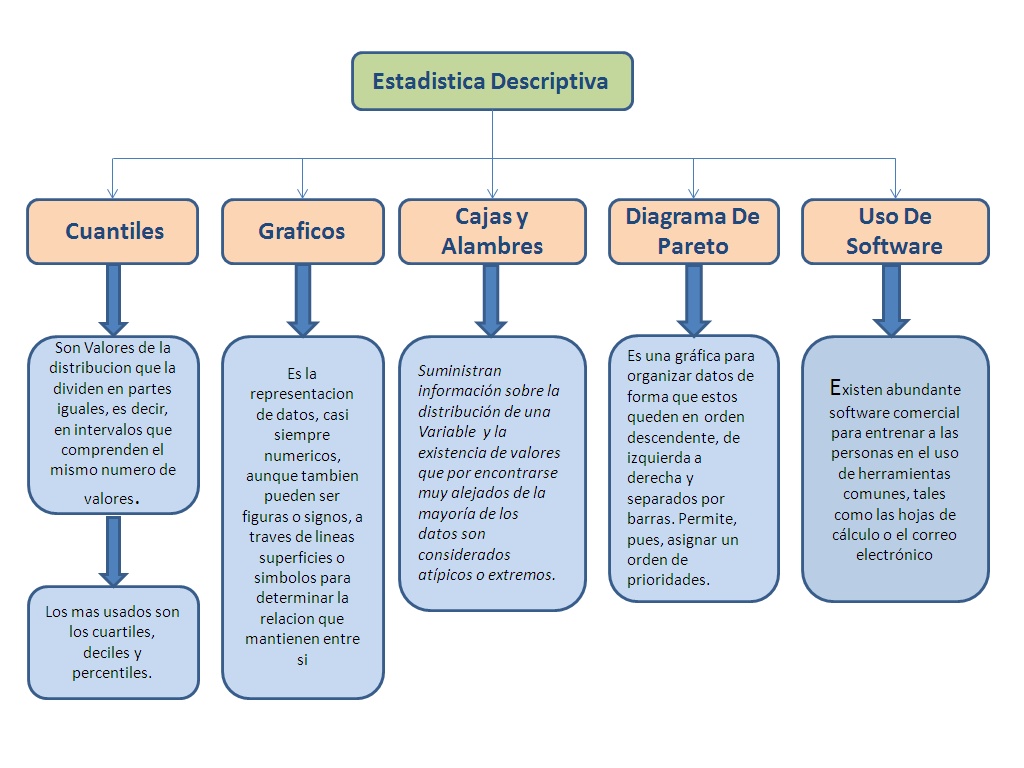
La Estadística se divide en dos ramas principales. Estadística Descriptiva resume y presenta datos. Estadística Inferencial hace inferencias sobre una población.
Parte 2: Estadística Descriptiva
La Estadística Descriptiva utiliza medidas de tendencia central. La media, mediana y moda son ejemplos. También utiliza medidas de dispersión como la varianza y la desviación estándar.
La media es el promedio de los datos. La mediana es el valor central. La moda es el valor más frecuente.
La varianza mide la dispersión alrededor de la media. La desviación estándar es la raíz cuadrada de la varianza. Son cruciales para entender la distribución de los datos.
Parte 3: Estadística Inferencial
La Estadística Inferencial usa muestras para inferir sobre poblaciones. El muestreo es el proceso de selección de una muestra. Se busca que la muestra sea representativa.
La inferencia estadística incluye la estimación de parámetros. También incluye la prueba de hipótesis. Estos procesos permiten generalizar resultados.
Una hipótesis es una afirmación sobre una población. La prueba de hipótesis determina si hay evidencia para rechazarla. Se utilizan valores p para tomar decisiones.
Parte 4: Probabilidad Avanzada
La probabilidad condicional considera la ocurrencia de un evento dado otro. Se denota como P(A|B). Significa la probabilidad de A dado que B ocurrió.
La independencia entre eventos implica que la ocurrencia de uno no afecta al otro. Formalmente, P(A|B) = P(A). Esto simplifica muchos cálculos.
El Teorema de Bayes relaciona probabilidades condicionales. Permite actualizar creencias a la luz de nueva evidencia. Es fundamental en la inferencia bayesiana.
Parte 5: Distribuciones de Probabilidad
Una distribución de probabilidad describe la probabilidad de cada valor posible de una variable aleatoria. Existen distribuciones discretas y continuas. Cada una tiene sus propias características.
Ejemplos de distribuciones discretas incluyen la Binomial y la Poisson. La Binomial modela el número de éxitos en ensayos independientes. La Poisson modela el número de eventos en un intervalo de tiempo.
La distribución Normal es una distribución continua muy importante. Aparece en muchos contextos. Está caracterizada por su media y desviación estándar.
Parte 6: Conexiones Clave
La probabilidad es la base de la Estadística Inferencial. Permite cuantificar la incertidumbre en las inferencias. Un buen entendimiento es crucial.
La Estadística Descriptiva proporciona el punto de partida. Resume los datos para identificar patrones. Estos patrones pueden guiar la inferencia.
El muestreo conecta la población con la muestra. Un buen diseño de muestreo es esencial. Garantiza la validez de las inferencias.