Calculo Diferencial Unidad 2 Limite De Fermat

Vamos a abordar un problema de Calculo Diferencial relacionado con el Limite de Fermat.

Comprendiendo el Problema

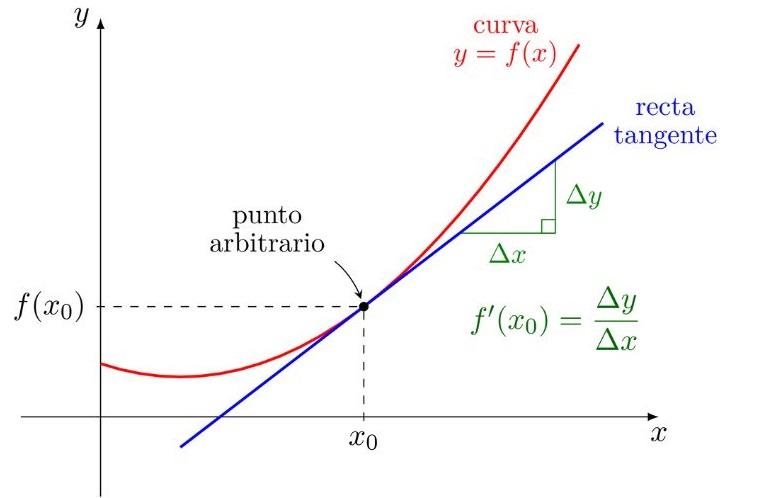
Primero, identifiquemos la forma del límite de Fermat. Generalmente, se presenta como un límite de la forma (f(x+h) - f(x))/h cuando h tiende a 0.

Nuestro objetivo es evaluar este límite. Para ello, necesitamos identificar la función f(x) en cuestión. Luego sustituimos en la expresión del límite.

Descomponiendo el Problema

El problema se divide en los siguientes pasos:

1. Identificar la función f(x).
2. Sustituir f(x+h) y f(x) en la expresión (f(x+h) - f(x))/h.
3. Simplificar la expresión algebraica resultante.
4. Evaluar el límite cuando h tiende a 0.

Ejemplo Práctico: f(x) = x²

Supongamos que f(x) = x². Necesitamos calcular el Limite de Fermat para esta función.

Calculamos f(x+h): f(x+h) = (x+h)² = x² + 2xh + h².

Sustituimos en la expresión del límite: ((x+h)² - x²)/h = (x² + 2xh + h² - x²)/h = (2xh + h²)/h.

Simplificación Algebraica

Simplificamos la expresión: (2xh + h²)/h = h(2x + h)/h = 2x + h.

Ahora evaluamos el límite cuando h tiende a 0: lim_h→0 (2x + h) = 2x + 0 = 2x.

Por lo tanto, el Limite de Fermat para f(x) = x² es 2x.

Otro Ejemplo: f(x) = x³

Consideremos ahora f(x) = x³. Similar al ejemplo anterior, calculamos el Limite de Fermat.

Calculamos f(x+h): f(x+h) = (x+h)³ = x³ + 3x²h + 3xh² + h³.

Sustituimos en la expresión del límite: ((x+h)³ - x³)/h = (x³ + 3x²h + 3xh² + h³ - x³)/h = (3x²h + 3xh² + h³)/h.

Simplificación y Evaluación

Simplificamos la expresión: (3x²h + 3xh² + h³)/h = h(3x² + 3xh + h²)/h = 3x² + 3xh + h².

Evaluamos el límite cuando h tiende a 0: lim_h→0 (3x² + 3xh + h²) = 3x² + 3x(0) + (0)² = 3x².

El Limite de Fermat para f(x) = x³ es 3x².

Consideraciones Finales

La clave para resolver problemas de Limite de Fermat radica en la correcta sustitución y simplificación algebraica. Recuerda factorizar el término h del numerador.

Practica con diferentes funciones para consolidar tu comprensión. Presta especial atención a las funciones polinómicas y trigonométricas.