Calculo De Volumenes Con La Integral Definida

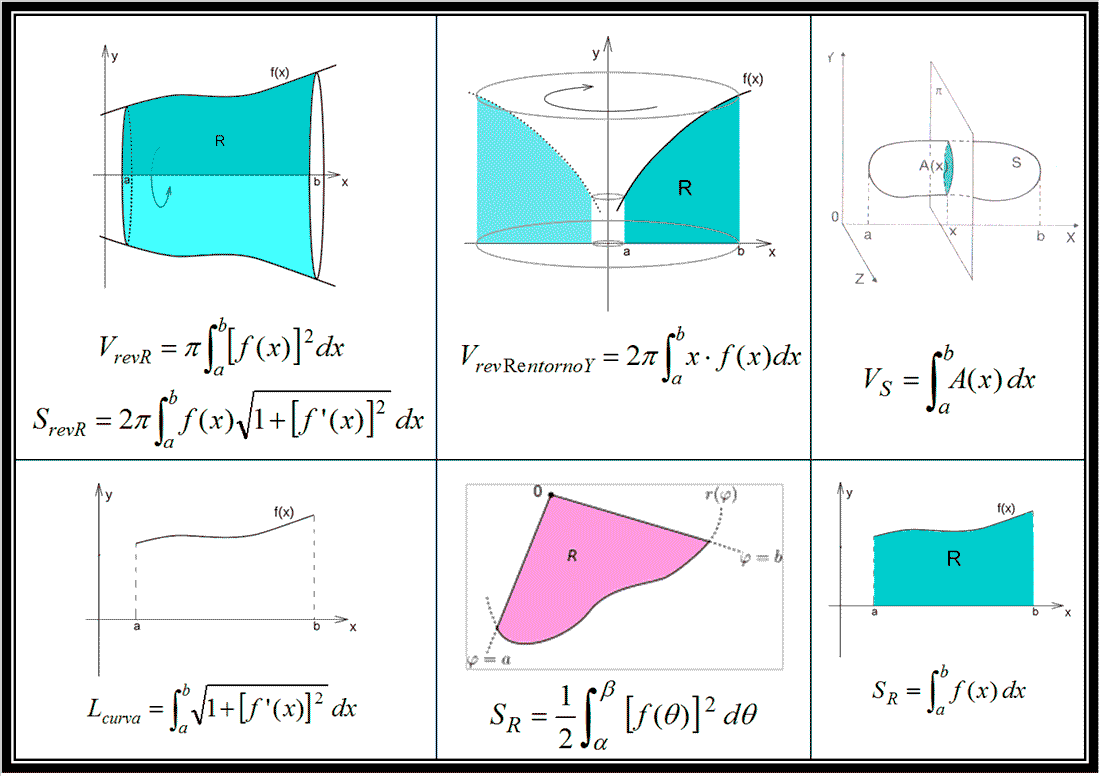
Calcular volúmenes utilizando la integral definida es una aplicación poderosa del cálculo integral. Nos permite determinar el volumen de sólidos con formas irregulares. En esencia, dividimos el sólido en secciones transversales infinitamente delgadas. Luego, sumamos los volúmenes de estas secciones.
El Método del Disco
Este método es útil cuando el sólido de revolución se genera al girar una región plana alrededor de un eje. Imaginemos que tenemos una función *f(x)*. Giramos la región bajo la curva desde *x = a* hasta *x = b* alrededor del eje x. Cada sección transversal perpendicular al eje x es un círculo (un disco).
El área de cada disco es *π[f(x)]2*. El volumen de cada disco es su área multiplicada por su espesor infinitesimal, *dx*. La integral definida que representa el volumen total es: ∫ab π[f(x)]2 dx.
Por ejemplo, calculemos el volumen de un cono. Un cono se puede generar girando una línea recta, *f(x) = rx/h*, alrededor del eje x. Aquí, *r* es el radio de la base y *h* es la altura del cono. Los límites de integración son de 0 a *h*. El volumen es: ∫0h π(rx/h)2 dx = (πr2h)/3.
El Método de las Arandelas
El método de las arandelas es una extensión del método del disco. Se utiliza cuando el sólido de revolución tiene un agujero en el medio. Esto ocurre cuando la región que se gira está delimitada por dos funciones, *f(x)* y *g(x)*, donde *f(x) ≥ g(x)*.
Cada sección transversal es una arandela (un círculo con un agujero en el centro). El área de cada arandela es *π[f(x)]2 - π[g(x)]2*. El volumen de cada arandela es su área multiplicada por su espesor infinitesimal, *dx*. La integral definida que representa el volumen total es: ∫ab π([f(x)]2 - [g(x)]2) dx.
Imagina girar la región entre *y = x2* e *y = x* alrededor del eje x. Aquí, *x ≥ x2* en el intervalo [0, 1]. El volumen del sólido resultante es: ∫01 π(x2 - (x2)2) dx. Resolviendo la integral obtenemos el volumen.
El Método de las Capas Cilíndricas
Este método es una alternativa a los métodos del disco y la arandela. A menudo es más fácil de usar cuando la región se gira alrededor del eje y o cuando la función es difícil de expresar en términos de *y*. En lugar de discos o arandelas, consideramos capas cilíndricas concéntricas.
Imagina que tenemos una función *f(x)* y giramos la región bajo la curva desde *x = a* hasta *x = b* alrededor del eje y. Cada capa cilíndrica tiene un radio *x*, una altura *f(x)* y un espesor *dx*. El volumen de cada capa cilíndrica es *2πxf(x)dx*.
La integral definida que representa el volumen total es: ∫ab 2πxf(x) dx. Este método requiere visualizar el sólido como una serie de capas concéntricas en lugar de secciones transversales perpendiculares al eje de rotación.
Por ejemplo, calculemos el volumen del sólido formado al girar la región delimitada por *y = x - x2* y el eje x alrededor del eje y. El volumen es: ∫01 2πx(x - x2) dx. Resolviendo la integral obtenemos el volumen.
Consideraciones Finales
La elección del método (disco, arandela o capas cilíndricas) depende de la forma del sólido y de la facilidad con la que se puede expresar la función. Es crucial identificar correctamente los límites de integración y la función que describe la forma del sólido. Practicar con diferentes ejemplos ayuda a comprender y aplicar estos métodos de manera efectiva. Recuerda que la integral definida es una herramienta poderosa para el cálculo de volúmenes en diversas situaciones.